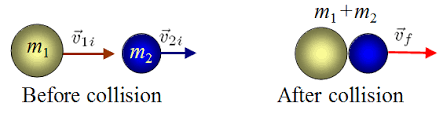UNIT 1
Jack Hughes
This Unit focused on measuring the motion of objects. We conducted experiments involving position over time, velocity over time, and acceleration. We also worked through the calculation of these values using Kinematic Equations.
Terminology - position, distance, and displacement
Position- Location at a specific time. Represented as “x”
Distance- How far you have gone, regardless of direction, and is always positive. It is a scalar.
Displacement- Overall change in position, including direction. Represented as “Δx”
Interpreting Position Time Graphs
In order to interpret a position time graph, it is important to first know that time, the independent variable, is measured on the x axis and position, the response variable, is measured on the y axis. The change in position over a given time is also known as the displacement. The y intercept of the graph is the position of an object when time is equal to zero. The slope of the Position Time Graph is representative of the velocity of the object, commonly measured in meters per second and it can be positive or negative. The steepness of the position time graph (absolute value of the slope) is the speed, or how fast the object is moving.
Determining velocity and speed from a Position Time Graph.
The slope of a position vs. time graph can be interpreted as the velocity of the object. It will have a positive or negative direction, and says how fast the object is moving in a given direction. The speed of the object will be the steepness of the slope, and shows how fast the object is moving, without direction.
Interpreting Velocity Time Graphs
The independent variable variable, time, is plotted on the x axis and the response variable, velocity, is plotted on the y axis. The slope of the velocity time graph is the acceleration of the object. The y intercept of the velocity time graph is the velocity of the object when the time is equal to zero, or the initial velocity.
Determining acceleration and starting velocity from a Position Time Graph
In order to determine the velocity time graph from the position vs. time graph, we need to take the derivative of the position vs. time graph and this value will give us the velocity time graph. (This could be as simple as the linear slope of the position time graph). When looking at the newly created velocity time graph from the derivative of the position vs. time graph, the velocity at time=0 is the initial, or starting velocity. The slope or derivative of this curve will be the acceleration of the object, and so the derivative of the velocity time graph will give you the acceleration.
Determining Position, Distance and Displacement from a Velocity Time Graph
The area underneath the velocity time graph at a given time is equal to the distance travelled at that given time. Through subtracting the area over the y axis from the area under the y axis the displacement can be calculated. The position can be determined through the derivative of the velocity time graph.
Connecting representations of motion: x-t graphs, v-t graphs, strobe diagrams etc.
In the gallery, I have attached some of the position time graphs and velocity time graphs from previous labs. The position time graph shows the position of an object over a given time, and it can also show the displacement of an object. It simply tracks where the object is at a given point in time. A velocity time graph is a representation of how fast an object is moving and in which direction it is moving. These graphs can also be linear or curved, and the derivative of a velocity time graph identifies the position time graph for that item. A strobe diagram can be used to measure the acceleration, and it can be visualized as if you were in a dark room and a light strobed, showing an object moving closer or further away from you at a given rate of acceleration.
Solving Problems using constant velocity and uniform acceleration models.
In order to solve problems with constant velocity and uniform acceleration, we have our three primary kinematic equations (I have attached them in the gallery). We have the variables change in time, initial position, final position, acceleration, initial velocity, and final velocity in these equations. When we have the value of three of these variables, it is possible to solve for the remaining ones by going through this system of equations.
Projectile Motion
A projectile is an object in the air that “is not touching” the air. It does not interact with the air and simply moves through the air. The velocity in the vertical direction is affected by the acceleration of gravity (-9.8m/s/s), and the velocity in the horizontal direction is constant. The upward velocity at which a projectile moves affects the horizontal distance that it travels. Also, the vertical motion determines the time the projectile spends in the air.
UNIT 2
Jack Hughes
This unit focused on forces, force calculations, and learning how different forces interact with objects and also how they act on different objects. We conducted experiments in order to calculate friction with a force sensor, we also used a set of experiments with mass and acceleration in order to derive Newton's Second Law.
(See the gallery for attached media)
Newton's First Law of Inertia
Newton's first law of inertia states that an object will continue to move at a constant velocity unless it feels an unbalanced push or pull from another force. This means that an object at rest will still be moving at a constant velocity (0 m/s) until an unbalanced force acts upon it. This relates to inertia, and we also discovered that the more mass an object has, the more inertia, or resistance to change in movement, that it has. In simple terms, the more mass that an object has, the more force that is needed to accelerate it.
Newton's Second Law of Acceleration, Net Force, and Mass
Newton's second law states that the acceleration of a system is proportional to the net force acting upon that system, and inversely related to the total mass of that system. As the net force acting upon a system increases (while mass is constant), than acceleration increases proportionately. As the total mass of the system increases (while net force is constant), then the acceleration decreases inversely. We studied this relationship in our unbalanced forces lab and came up with the formula: acceleration (m/s/s)= net force (N)/total mass (kg). We are able to use this equation to solve for some of the unknowns within a system when looking at different force scenarios.
Newton's Third Law
Newton's Third Law states that whenever there is an interaction between two objects, there is a force acting upon both of the objects. This force is equal in magnitude, and opposite in direction. It is the relationship between two objects where they feel one interaction. One example is where a person runs up and shoves another person. The person who shoves the other person exerts the applied force, but the body of the person being shoved also exerts an equal and opposite force against the shove on the shover's hands.
Identifying Interactions: System Schema/ Force Diagrams
The first step in attacking a force problem in physics is to draw out the situation and the information is given. All of the objects of interest are drawn in bubbles, and connected by the forces between the objects in a system schema. Gravity is represented by a dotted line because it is not a contact force. Once all of the forces are drawn connecting the objects in a system schema, we the can create a force diagram, in which the object of interest is represented by a dot, and the forces with respective magnitudes and directions are drawn from the dot. We label these vectors by naming the force by (something) on (the object of interest).
In order to identify the type of forces between an object, we look for which objects are involved and reference our one note with the definitions of what kind of forces can act between objects. Some commonly occurring forces this unit were Fg, FF, FN, FA, and FT.
Force Calculations/Force Problems
These two concepts work well together in one section. In order to solve force problems, we use a combination of different critical thinking ideas, definitions, and equations to solve for the information we are lacking. We know that
Net Force- sum of all of the forces acting in a system in a given direction
Net force= mass x acceleration
Spring Force= -(k)(delta x) where k is the spring constant and delta x is the amount of stretch, in meters.
mew= FF/FN where mew is the coefficient of friction
Fg= mass x g where g= -9.8m/s/s
as well as our kinematic equations from unit 1
Through using these equations and the variables we are given, we are able to solve for what we do not have. What has proved to be especially important is our definition that net force is the sum of all forces. It allows us to solve for the net force and then use that to solve for acceleration if all we are given is the mass of an object. We can make a force table and solve for this information. From there, it is possible to plug that equation into our kinematic equations and solve for other unknown variables. The calculations for force problems consist of manipulating the equations and definitions we have learned in order to solve for the unknown. A very helpful component of solving force problems is drawing out a system schema, a force diagram, and a force table in order to really discover what we are searching for.
Relating Representations of Motion and Force Models
Force Diagrams are used in order to represent the motion of the object of interest. This can be attributed to Newton's first law- an object will remain at rest until an unbalanced force acts upon it. By showing the unbalanced forces in a force model, it displays that the object will be in motion.
Solving Problems with Forces and Motion
These types of problems are interesting because it allows us to tie together many of the key equations and concepts we have learned so far in order to calculate many things that are going on in a system. When an object is in motion, we know that there are unbalanced forces acting upon it. When given the net force, we can solve for what force is acting in what direction using the definition of net force. When given the mass, we can solve for the force of gravity using the gravitational constant and also then possibly solve for the acceleration of the forces if the magnitude of the force is given. When we do not know what the acceleration of the system is, we can use kinematic equations to solve for acceleration because the object is in motion. It is an integration of both unit 1 and unit 2.
UNIT 3
Jack Hughes
The third unit covered the components of circular motion. We learned about acceleration in two dimensions in order to build off of our knowledge of one dimensional acceleration. We learned about centripetal acceleration and the relationship between forces and acceleration in circular motion. We performed the Whirly Durly Lab in class this unit (See Labs Page) and discovered the relationship between the velocity of a system and centripetal acceleration. We ended the term with Universal Gravitation and the orbit of objects and relative gravity.
Uniform Circular Motion
We learned about many different facets of circular motion this term. We began by talking about polar coordinates, and learning how to covert between Cartesian and polar coordinates. Some formulas that we explored for this were:
x coordinate= Radius(Cosine Theta)
y coordinate = Radius(Sine Theta)
Radius= Sqrt(x^2+y^2)
Theta=arctan(y/x)
We then explored this concept in a little more depth, and talked about angular displacement and arc length, or the distance travelled along a circular path. Because Circumference is equal to 2(pi)(r), to find a fraction of the distance traveled we can use the equation:
s= radius(theta, in radians) where s= arc length.
Angular speed can be written as:
Omega= (change in theta)/(change in time)
The tangential speed of an object is known as the speed of the object moving tangent to the arc it is traveling along. An equation that we derived that shows the relationship between angular and tangential velocity is:
omega x radius = tangential velocity
This builds off of our existing knowledge of one dimensional velocity, because we were always working in terms of one dimension until this unit.
After introducing the circular velocity components, we began to ask questions about velocity. Because the objects are traveling along a circular path, they are always accelerating because they are constantly changing direction. We conducted the whirly durly lab and discovered the relationship of centripetal acceleration to be
ac= v^2/r
From here, we are able to use previous knowledge of net force to solve equations using mass, speed, time, and tangential velocity to solve physics problems.
Universal Gravitation
In unit 3, we discovered that the model Fg= mg is incomplete and there is a more refined way of solving for the force of gravity. Through an in-class investigation, we also discovered that the inverse square model represents the relationship between the force of gravity and radius between two masses.
The Law of Universal Gravitation states that Gravity is proportional to the mass of each body and inversely proportional to the square of the distance between the two bodies. This equaition can be written as:
Fg= (G(m1)(m2))/r^2
and the universal gravitational constant is 6.67 x 10^-11
To find the field strength of Earth's gravitational field, we use the equation:
g= Fg/m = (Gmp)/rp^2
By combining the info we learned regarding centripetal acceleration, we can solve gravitational field problems as well as problems about satellites orbiting planets. Overall, this unit was very fun and gave a great application into centripetal acceleration and how circular motion works around us every day.
UNIT 4
Jack Hughes
The fourth unit that we learned this year involved an introduction to energy. In specific, we began the unit by learned about the different types of energy that exist in the universe, such as kinetic, electrical, thermal, chemical, light energy, and various types of potential energy. e defined energy as "the stuff we need to do stuff/make changes to the universe." We did an energy skate park simulation where we developed that energy is neither created or destroyed, only conserved. This led to our development of LOL charts and the conservation of energy equations that we created. We learned that energy could enter or leave our systems, and developed the idea of working (W), heating (Q), and radiating (R). Then, we did a mini lab about power where we did various physical tasks to test our own personal power. We did some calculations with the relationships we learned and developed, and then we finished our unit with Universal Gravitational potential energy. During this unit, we had 3 substantial assignments. Mastering Physics 4.1, 4.2, and a Unit 4 quiz. There is not much multimedia for this unit, but there are a few applicable photos in the attached gallery.
Representing Energy Transfers with Bar (LOL) Charts
The LOL chart was a powerful tool that we learned about in order to have a qualitative understanding of energy transfers both within a system and energy that was entering or exiting a system. Bars on an LOL chart represent the amount of energy and what kind of energy is in a system at the initial and final positions. The O in LOL charts is used to define what our system is, and what type of energy is entering or exiting the system, if any. As defined in my introduction, the three types of energy transfers that can occur outside of the system are W, Q, and R. We draw arrows facing the direction where the energy is going in the O. Ultimately, this allows us to create conservation of energy equations that are very easy to understand. It is a good visual tool to use to set up all systems.
Energy Problem Solving
There are a few key ideas that should be employed when trying to solve problems related to energy that have various unknowns. Upon looking at a problem, the first thing that we should do is make an LOL chart, which I just previously covered. After we do that and can visualize how the energy is being transferred, we can begin to use some of the equations we derived and developed.
Elastic Potential Energy= (1/2)(k)(delta x)^2
Gravitational Potential Energy= mgh
Kinetic Energy= (1/2)(mv^2)
Work= Force x Displacement
By using these equations to our advantage, we are able to solve most energy problems.
Work
Work happens when energy is transferred by an external push or pull that is exerted onto a system. This is most commonly referred to as a force. Work must be included in our conservation of energy equations in order to account for no energy being created or destroyed. As previously stated, the equation we can use to solve for how much work is done on a system is:
Work = Force x Displacement
Power
Power is the rate at which energy is transferred, or the rate of doing work. The equations for power are:
Power = W/delta t
Power = change in energy/ change in time
Power is measured in a unit called Watts, of which one watt is equal to an energy transfer of 1 Joule per second. We did our exercise lab to determine who in the class was the most powerful, and two key concepts that we learned were that two ways something can become more powerful is to transfer more energy in the same amount of time or to transfer the same amount of energy in less time.
Relating Energy/Work/Power to Forces and Motion
All of these concepts are interconnected within the context of this unit. Forces are the things that cause work to happen, and force is also what causes motion. Work is a transfer of energy, and the rate at which energy is transferred is power. Knowing these definitions will allow me to maximize the critical thinking skills I need to solve for various unknowns.
Connecting Representations of Motion with Representations of Forces
In a force vs. displacement graph, the area under the curve corresponds to the amount of energy transferred in an interaction. This can be especially helpful in quantifying the amount of energy in order to solve for various unknowns within a conservation of energy equation.
Extra Notes:
Energy is the stuff that we need to make stuff happen.
Energy is measured in the unit Joules. Not Newtons!
The Law of Conservation of energy states that energy in the universe is never created or destroyed, only transferred. In other words, there is a finite amount of energy in the universe and it is constantly being transferred between systems and objects.
Work is the most common form of energy transfer that we will work with in this unit, but still be cognizant of heating and radiating energy transfers because not every transfer is work.
For some problems on mastering physics 4.2, it was valuable knowledge to remember that the gravitational force and normal force are equivalent. This can help if you get stuck on problems that involve frictional forces so that you can solve for Mew.
UNIT 5
Jack Hughes
The fifth unit that we learned this year was Momentum. Firstly we learned about explosions and did a min activity with a plunger cart and another cart where we released the plunger and changed the masses of each cart and saw the changes in kinetic energy. Then, we followed that by learning about collisions - inelastic and elastic - by using two carts with varying masses with either magnets so the carts "bounced" or Velcro so the carts "stuck" and calculated how mass and velocity affected the movement of the object and how easy it was to stop. This brought us to the concept of momentum. Using LIL charts, we learned how to do momentum problems. Finally, we learned about the importance of the center of mass regarding momentum. The required assignments for this unit was Mastering Physics 5.1 and 5.2; See attached gallery for relevant media.
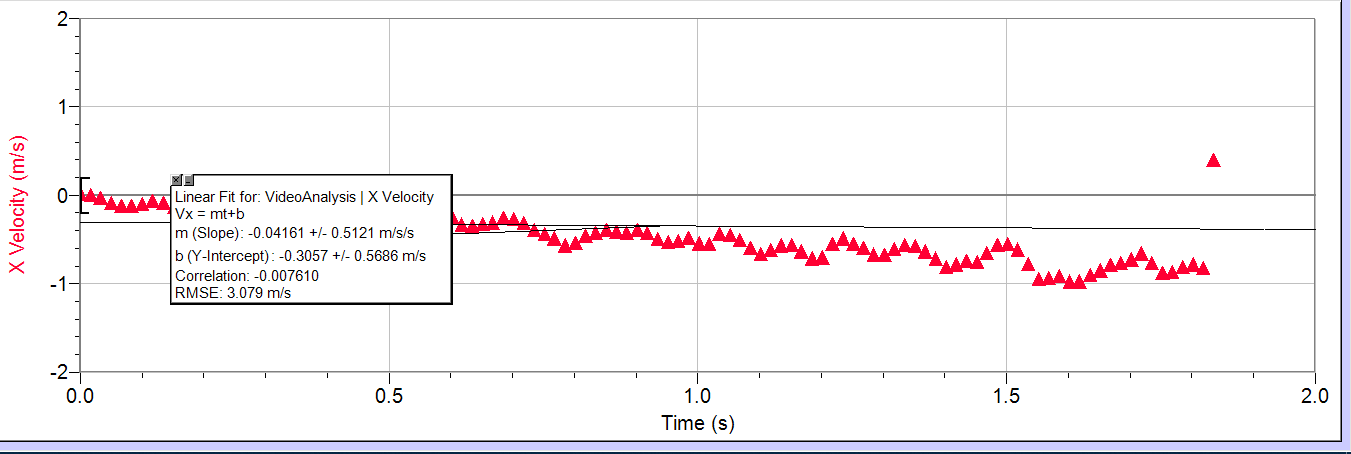
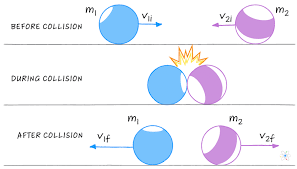
Types of Collisions (Elastic, Inelastic, etc.)
There are 4 types of collisions that we learned about- Elastic, Inelastic, Perfectly Inelastic, and Explosions.
- Elastic: "hard" collisions where no kinetic energy is lost. This is similar to saying it is as if the objects "bounce off of each other.
- Inelastic: Physical deformation happens during this collision, such as a bullet hole when a gun shoots at a target, and kinetic energy is lost. Kinetic energy can also be lost in the form of thermal energy in these types of collisions, too.
- Perfectly Inelastic: Two objects stick together in order to move together as one object. This is a deformation and kinetic energy is lost. A common example we looked at was when the two carts with Velcro hit each other and became one object and slowed down.
- Explosions: Because explosions are a product id built up potential energy, and explosion increases in potential energy.
Impulse (Definition, graphical relationships, eq., etc)
Impulse is defined as the change in momentum. It can be represented by the variable j or by delta p. In order to solve for impulse, we can use the equations:
J= P final - P initial
J= (Net Force) x (change in time)
A graphical representation of impulse that is very important to remember is that the area under the Force vs. Time graph is the impulse on an object. Lastly, it is important to note that impulse is equal and opposite.
Momentum (Bar Charts, definitions, etc.)
Momentum is the measure of how hard it is to stop an object's motion. To calculate momentum, we use the variable p for momentum and the equation:
p= Mass x Velocity
Using our knowledge of collisions, we are able to represent our understanding of a given physics scenario in an LIL chart.
An LIL chart consists of three parts: the initial momentum of the system, the impulse, and the final momentum of the system. On all parts of the graph, momentum can be either positive or negative and it helps display where the momentum is going, how it is changing, and how it is being transferred inside and outside of a system.
Conservation of Momentum (include Center of Mass)
Momentum is conserved in elastic collisions- therefore pi=pf for elastic collisions. Also, the center of mass of a system will always have the same momentum that remains unchanged. When collisions occur in two dimensions, momentum in each dimension is conserved. That is,
pxi=pxf
pyi=pyf
Another way that this equation can be written when there is an impulse is that
pi + J = pf
Relating Momentum Energy, Forces, and Kinematics
When doing mastering physics, there were many problems that stumped me at first glance. I started to look over some kinematic equations and it really helped me. In order to solve for the net force, we can use the w= net force x displacement when we are able to calculate how much energy is transferred, and use that with time to calculate impulse and ultimately momentum. These three topics are inter connected and any of the equations can help me find an unknown in a scenario if applied correctly.